Tópicos Especiais em Algoritmos Ciência da Computação
Grafos
A Teoria dos Grafos possui enorme importância, servindo como modelo de diversos problemas. Alguns desses problemas possuem soluções eficientes, enquanto outros não.
Esta teoria tem uma terminologia específica, que por si só, merece ser estudada a parte.
O material complementar, disposto aqui pode ajudar com isso.
A seguir, será assumido que o leitor tem familiaridade com os conceitos básicos de grafos.
Percurso em Grafos
Uma série de problemas podem ser resolvidos apenas sabendo como caminhar em grafos. Exploraremos algumas aplicações dos diferentes tipos de travessia em grafos nesta seção.
Busca em Profundidade
A busca em profundidade (DFS - Depth First Search) inicia de um nó $u$ e procede recursivamente a um dos seus vizinhos não visitados. Quando a DFS chega a um nó em que não pode prosseguir recursivamente, ela retrocede (realiza o backtrack) ao nó pai, presente na chamada da função anterior.
Em uma implementação baseada em listas de adjacências, a busca em profundidade poderia ser implementada da seguinte maneira.
#include <bits/stdc++.h>
using namespace std;
enum{NOT_VISITED,VISITED};
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
/***
* Lista de adjacências de um grafo. Cada aresta é representada com um par,
* contendo o nó destino e o peso da aresta. No caso de grafos sem peso, o
* segundo membro do par pode ser ignorado
***/
vector<vii> adj_list;
/***
* dfs_num marca se um nó foi visitado ou não. Deve ser utilizado em uma
* busca em profundidade para que ela não proceda a nós que já
* foram visitados de modo a evitar um laço infinito. Inicialmente,
* deve ser inicializada com NOT_VISITED
***/
vi dfs_num;
/***
* Busca em profundidade, parte de um nó u e, para cada vizinho não visitado,
* faz a chamada recursiva para este vizinho.
***/
void dfs(int u){
dfs_num[u] = VISITED;
for(auto& v: adj_list[u]){
if(dfs_num[v.first]==NOT_VISITED){
dfs(v.first);
}
}
}Como a busca em profundidade olha para cada vértice e cada extremidade de cada aresta uma única vez, sua complexidade é $\Theta(\lvert V\lvert +\lvert E\lvert)$ quando implementada em listas de adjacências e $\Theta(\lvert V\lvert ^2)$ sobre matrizes de adjacências.
Analogia com Backtracking
De fato, um backtracking pode ser visto como uma busca em profundidade, no entanto, tipicamente em um backtracking os nós, ou estados, são marcados como não visitados quando há o retrocesso, possibilitando uma visita em uma chamada recursiva futura. Por conta disso, enquanto a complexidade da busca em profundidade é linear no número de vértices e arestas, quando usando listas de adjacências, a complexidade do backtracking é exponencial.
O pseudocódigo abaixo deixa claro as similaridades entre uma DFS e um código baseado em backtracking partindo de um estado $s$.
- Se $s$ é um estado final ou um estado inválido, retorne adequadamente.
- Para cada configuração vizinha derivada do estado $s$
- Chame recursivamente a função para a configuração vizinha.
Exemplo: UVa 11902
No problema Dominator (UVa 11902), recebe-se como entrada uma matriz de adjacências e deseja-se saber, dado um vértice $u$ quais são os vértices que são dominados por ele. Um vértice $a$ domina um vértice $b$, quando não existem caminhos do vértice origem $0$ que cheguem em $b$ e não passem por $a$. Por definição, todo nó alcançável da origem domina ele mesmo.
Na figura abaixo, temos que o nó $3$ domina o nó $4$, mas que o nó $1$ não domina o nó $3$, uma vez que existe um caminho alternativo a partir do nó $0$, que passa pelo nó $2$ e chega ao nó $3$.
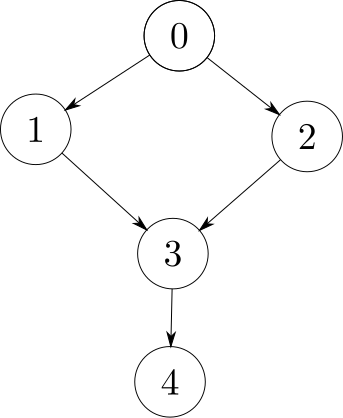
Como neste problema $\lvert V\lvert \leq 100$, um algoritmo cúbico é o suficiente para construção de uma solução. A ideia é, partir da origem, marque, através de uma DFS, todos os nós alcançáveis da origem como visitados. Para cada nó $x$ visitado a partir da origem, excluímos $x$ do grafo e repetimos a consulta a partir da origem. Um vérticed $y$ não é dominado por um vértice $x$ se:
- Não é alcançável a partir da origem, ou
- Após a exclusão de $x$, $y$ é alcançável a partir da origem.
Se nenhuma das condições acima se aplica, $y$ é dominado por $x$. Para resolver o problema, basta aplicar este procedimento para cada nó $x$ do grafo. Ao todo, tem-se tempo $\Theta(\lvert V \lvert \cdot \lvert V \lvert^2) = \Theta(\lvert V \lvert ^ 3)$.
Observação: não é necessário efetivamente modificar a estrutura do grafo e deletar vértices. Basta marcar $x$ como já visitado antes de aplicar a DFS.
Busca em Largura
A partir de um nó de origem $u$, a busca em largura (BFS - Breath First Search) primeiramente visita todos os vizinhos imediatos de $u$ (primeiro nível). Após visitar todos o nós do primeiro nível ela procede para todos os vizinhos dos nós que se encontram no primeiro nível (segundo nível), isto é, os vizinhos dos vizinhos de $u$, e assim por diante.
Essa busca pode ser implementada com o auxílio de uma fila. Inicialmente, para coloca-se o nó de origem na fila $Q$ e:
- Enquanto $Q$ não está vazia.
- Retire o nó $x$ da frente da fila.
- Para cada vizinho $y$ de $x$, se $y$ não está visitado, coloque-o na fila.
- Marque $x$ como visitado.
Esta estratégia pode ser exemplificada com o código abaixo.
#include <bits/stdc++.h>
using namespace std;
const int INFINITY{ numeric_limits<int>::max() };
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
/***
* Estrutura que diz a distância para o nó de origem.
* Inicialmente inicializada com Infinito;
***/
vi d;
/***
* Lista de adjacências de um grafo. Cada aresta é representada com um par,
* contendo o nó destino e o peso da aresta. No caso de grafos sem peso, o
* segundo membro do par pode ser ignorado
***/
vector<vii> adj_list;
/***
* Busca em largura partindo de um nó u. Inicialmente, visita-se
* os vizinhos de u, depois os vizinhos dos vizinhos de u, e assim por diante.
* Uma fila é utilizada para implementar este comportamento
***/
void bfs(int u){
queue<int> q;
q.push(u);
while(!q.empty()){
int x = q.front();
q.pop();
for(auto& y: adj_list[x]){
/**
* Se a distância até y.first é infinito,
* significa que ele não foi visitado
**/
if(d[y.first]==INFINITY){
d[y.first] = d[x]+1;
q.push(y.first);
}
}
}
}Nesta busca, utiliza-se um vetor de distância a partir da origem para determinar se um nó foi visitado ou não. Caso a distância da origem para o nó esteja como infinito, significa que ele ainda não foi visitado. De brinde, esta busca em largura resolve o problema do menor caminho partindo de uma origem em um grafo sem pesos nas arestas, uma vez que, quando um nó é inserido na fila, a distância da origem para ele é atualizada como sendo a distância da origem ao nó pai mais um.
Componentes Conexas
Dado um grafo não-direcionado, um problema recorrente é segmentar este grafo em suas componentes conexas. Uma componente conexa de um grafo não-direcionado é simplesmente um conjunto de vértices que se alcançam.
Para achar as componentes conexas, basta aplicar uma busca em profundidade, ou em largura, a cada nó não visitado, conforme código abaixo, em que se utiliza uma DFS para tal.
void connected_components(){
int n = 1;
for(size_t i=0;i<adj_list.size();i++){
if(dfs_num[i]==NOT_VISITED){
cout << "Component #" << n << ": ";
dfs(i);
n++;
cout << endl;
}
}
}
void dfs(int u){
cout << u << " "; // imprime-se um nó da i-ésima componente
dfs_num[u] = VISITED;
for(auto& v: adj_list[u]){
if(dfs_num[v.first]==NOT_VISITED){
dfs(v.first);
}
}
}Flood-Fill
Uma variação do problema de achar as componentes conexas de um grafo é o problema do Flood-Fill, que geralmente age sobre o domínio de grafos implícitos 2D.
Tomando o problema UVa 469 como base, é dado um grid 2D contendo os caracteres W (água) e L (terra). Em seguida são dadas coordenadas do grid contendo posições de células com água. Para cada uma dessas posições, deve ser computada a área do lago contendo aquela posição de água. A área do lago simplesmente pode ser vista como o número de posições com água alcançáveis a partir da posição original considerando vizinhanças verticais, horizontais e diagonais.
Por exemplo, para a entrada
1
LLLLLLLLL
LLWWLLWLL
LWWLLLLLL
LWWWLWWLL
LLLWWWLLL
LLLLLLLLL
LLLWWLLWL
LLWLWLLLL
LLLLLLLLL
3 2
7 5
As respostas são $12$, uma vez que a partir da célula $(3,2)$, é alcançado um total de $12$ células com W, e $4$, pois através da célula $(7,5)$, é possível alcançar $4$ células com W.
/**
* Coordenada das movimentações
**/
int dr[] = {1,1,0,-1,-1,-1, 0, 1};
int dc[] = {0,1,1, 1, 0,-1,-1,-1};
/**
* @brief Flood-fill em um tabuleiro RxC
* @param r número da linha
* @param c número da coluna
* @param c1 caractere de água
* @param c2 caractere a substituir o caractere da água
* @return Retorna a área do lago formado a partir da célula (r,c)
*/
int floodfill(int r, int c, char c1, char c2) {
// Se está fora do grid, a área é 0
if (r < 0 || r >= R || c < 0 || c >= C) return 0;
// Se a célula não é uma posição com água, a área é 0
if (grid[r][c] != c1) return 0;
// Caso contrário já temos área do lago igual a 1
int ans = 1;
// Marca a posição (r,c) como visitada
grid[r][c] = c2;
// Aplica a busca em profundidade (flood-fill) nas adjacências
for (int d = 0; d < 8; d++)
ans += floodfill(r + dr[d], c + dc[d], c1, c2);
// Retorna a área total do lago
return ans;
}Ordenação Topológica
Um DAG é um grafo dirigido e acíclico. Para muitos problemas que envolvem grafos, não se conhece soluções eficientes (tempo polinomial) quando a entrada é um grafo qualquer, no entanto, quando restringe-se o tipo da entrada para um DAG, o problema passa ter uma solução eficiente. Um exemplo disso é o problema do maior caminho, que sabidamente é um problema $\mathcal{NP}$-completo, mas que, quando a entrada restrige-se a DAGs, pode ser resolvido em tempo linear no número de vértices e arestas.
Nestes problemas restritos a DAGs, algumas soluções necessitam realizar uma ordenação topológica antes de qualquer coisa. Esta ordenação tem como objetivo estabelecer uma ordem entre vértices de forma que, se existe uma aresta $(u,v)$, então obrigatoriamente, $u$ sempre tem que vir antes de $v$. Dado um DAG, é possível ter múltiplas ordenações topológicas válidas, mas normalmente, qualquer uma delas serve para construir a solução. Além disso, é sempre garantido que é possível obter uma ordenação topológica, uma vez que um DAG não tem ciclos.
A ordenação topológica pode ser realizada com uma pequena adaptação na busca em profundidade. Suponha um nó $u$, obrigatoriamente, todos os vizinhos de $u$ devem estar após ele na ordenação topológica, então, basta inserir $u$ antes de todos os seus vizinhos.
O código a seguir utiliza uma busca em profundidade para computar uma ordenação topológica inversa. Para um nó $u$, ele insere este nó em um vetor somente após aplicar a busca em profundidade para todos os seus vizinhos, que estarão antes de $u$ no vetor. Para obter a ordenação topológica, basta inverter o vetor.
#include <bits/stdc++.h>
using namespace std;
enum{NOT_VISITED,VISITED};
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
/***
* Lista de adjacências de um grafo. Cada aresta é representada com um par,
* contendo o nó destino e o peso da aresta. No caso de grafos sem peso, o
* segundo membro do par pode ser ignorado
***/
vector<vii> adj_list;
/***
* dfs_num marca se um nó foi visitado ou não. Deve ser utilizado em uma
* busca em profundidade para que ela não proceda a nós que já
* foram visitados de modo a evitar um laço infinito. Inicialmente,
* deve ser inicializada com NOT_VISITED
***/
vi dfs_num;
/**
* tp é o vetor contendo a ordem dos vértices segundo a ordenação
* topológica
**/
vi tp;
/***
* Busca em profundidade, parte de um nó u e, para cada vizinho não visitado,
* faz a chamada recursiva para este vizinho.
***/
void dfs(int u){
dfs_num[u] = VISITED;
for(auto& v: adj_list[u]){
if(dfs_num[v.first]==NOT_VISITED){
dfs(v.first);
}
}
tp.push_back(u);
}
// reverse(tp.begin(),tp.end()) Como a ordenação topológica é baseada na DFS, também leva tempo $\Theta(\lvert V \lvert + \lvert E \lvert)$
Outra forma de calcular a ordem topológica é através do algorithmo de Khan. Este algoritmo usa uma fila $Q$ e coloca os vértices em ordem em um vetor $tp$ da seguinte maneira:
- Insira os vértices com in-degree 0 na fila $Q$.
- Enquanto $Q$ não estiver vazia:
- Retire o nó $u$ da frente da fila e o insira no vetor $tp$
- Para cada vizinho $v$ de $u$, subtraia $1$ de seu in-degree. Caso o in-degree de $v$ passou a ser $0$, coloque-o na fila.
Uma aplicação clássica de ordenação topológica é estabelecer a ordem de cumprimento de matérias, dado relações de pré-requisito entre elas, de uma determinada matriz curricular.
Checagem de Bipartição
Um grafo é dito bipartido se o seu conjunto de vértices pode ser divido em duas partições $V_1$ e $V_2$ com $V_1 \cup V_2 = V$ e $V_1 \cap V_2 = \emptyset$ de modo que não existem arestas que liguem vértices de $V_1$ ou de $V_2$ entre si. Em outras palavras, Se $(u,v\in V_1) \lor (u,v \in V_2) \implies (u,v) \notin E$.
A figura abaixo ilustra um grafo bipartido.
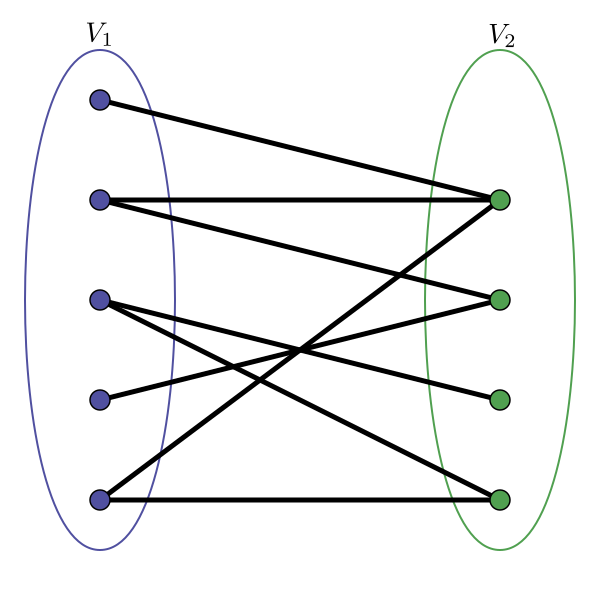
Tomando o problema UVa 10004 como estudo de caso, deseja-se saber se um grafo pode ser colorido com duas cores, em outras palavras, determinar se um grafo é bipartido.
Este problema pode ser resolvido tanto com uma BFS quanto uma DFS. Com a BFS assumimos que os vértices não visitados possuem cor branca, os vértices da partição $V_1$ cor azul e os vértices de $V_2$ cor vermelha. Para detectar se de fato o grafo não é bipartido fazemos:
- Pinte todos os vértices de branco
- Escolha um vértice e pinte-o de vermelho
- Coloque esse vértice em uma fila $Q$
- Enquanto $Q$ não está vazia.
- Retire o vértice $u$ da frente de $Q$
- Se existe algum vizinho da mesma cor de $u$, o grafo não pode ser bipartido.
- Caso contrário, pinte todos os vizinhos brancos (não visitados) da cor oposta de $u$, isto é, se $u$ é azul, pinte seus vizinhos de vermelho, e se $u$ é vermelho, pinte os seus vizinhos de azul.
- Coloque os vizinhos de $u$ na fila.
Adaptando o código anterior da busca em profundidade, temos o código abaixo.
#include <bits/stdc++.h>
using namespace std;
enum{WHITE=-1,BLUE=0,RED=1};
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
/***
* Estrutura que diz a cor do nó.
* color[u] = -1 se u é branco, isto é, não foi visitado.
* color[u] = 0 se u é azul
* color[u] = 1 se u é vermelho.
* Inicialmente todos os nós são brancos
***/
vi color;
/***
* Lista de adjacências de um grafo. Cada aresta é representada com um par,
* contendo o nó destino e o peso da aresta. No caso de grafos sem peso, o
* segundo membro do par pode ser ignorado
***/
vector<vii> adj_list;
/**
* @brief Busca em largura partindo de um nó u para verificar se um
* grafo é bipartido.
*
* @param u nó inicial
* @return true se o grafo é bipartido
* @return false se o grafo não é bipartido.
*/
bool bfs(int u){
queue<int> q;
// u é pintado de vermelho e colocado na fila0
q.push(u);
color[u] = RED;
while(!q.empty()){
int x = q.front();
q.pop();
for(auto& y: adj_list[x]){
/***
* Se a cor do vizinho de x é branca, ele é pintado da cor
* oposta de x
***/
if(color[y.first]==WHITE){
color[y.first] = 1-color[x];
q.push(y.first);
}
/***
* Se x e seu vizinho y tem a mesma cor, o grafo não
* pode ser bipartido
***/
else if(color[y.first]==color[u]){
return false;
}
}
}
return true;
}Componentes Fortemente Conexas
Dado um grafo direcionado, dizemos que dois vértices $u$ e $v$ estão na mesma componente fortemente conexa se existe um caminho de $u$ para $v$ e existe um caminho de $v$ para $u$.
Para realizar a detecção de componentes fortemente conexas, é possível utilizar o algoritmo proposto por Tarjan em 1972. Ele consiste em utilizar uma única DFS para armazenar todas as componentes fortemente conexas. Nesta DFS, o algoritmo se preocupa em preencher, para cada nó $u$, duas estruturas de dados:
- $\mathtt{dfs\_num[u]}$: o número de visitação do nó em uma DFS.
- $\mathtt{dfs\_low[u]}$: o nó com $\mathtt{dfs\_num[u]}$ mais baixo que $u$ consegue alcançar.
Tome um nó $v$ qualquer, tal que $\mathtt{dfs\_num[u]} = \mathtt{dfs\_low[u]}$, através deste algoritmo é possível concluir que, todos os outros nós $w$ que possuem $\mathtt{dfs\_low[w]} = v$, estão na mesma componente fortemente conexa de $v$. Isto é verdade pois, se um nó $w$ está na mesma componente fortemente conexa de $v$, o nó com menor $\mathtt{dfs\_num[v]}$, $\mathtt{dfs\_low[w]} = v$ por definição de componente fortemente conexa, uma vez que deve existir um caminho de $w$ para $v$ também!
Para preencher a estrutura de dados $\mathtt{dfs\_low[u]}$ para cada nó $u$ devemos utilizar o conceito de back-edge. Se durante uma DFS, existe uma aresta $(u,v)$ e $v$ ainda não foi visitado, então o menor nó alcançável por $u$ é o mínimo entre o menor nó alcançável por $u$ e o menor nó alcançável por $v$. Caso $v$ tenha sido visitado, porém não finalizado, isto é, nem todos os vizinhos de $v$ foram processados pela DFS, significa que a aresta $(u,v)$ é uma back-edge, e portanto, existe um ciclo! Neste segundo caso, o menor nó alcançável por $u$ é o mínimo entre $\mathtt{dfs\_low[u]}$ e $\mathtt{dfs\_num[v]}$, o número de DFS de $v$
Isso é ilustrado pelo seguinte algoritmo.
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
enum{WHITE=0,GREY=1,BLACK=2};
// Variáveis globais
int dfs_n = 0; // Numeração da DFS
vector<vi> g; // Lista de adjacências
vi dfs_num; // Estrutura dfs_num
vi dfs_low; // Estrutura dfs_low
vi visited; // Marca o estado do vértice
stack<int> st; // Pilha para armazenar a componente fortemente conexa
/**
* @brief A partir de um nó u, computa as componentes fortementes conexas
* dos nós alcançáveis a partir de u
*
* @param u Nó inicial.
*/
void scc(int u) {
dfs_num[u] = dfs_low[u] = dfs_n;
dfs_n++;
// Marca o nó como em processamento
visited[u] = GREY;
// Insere o nó na pilha
st.push(u);
for (auto v : g[u]) {
// Para cada aresta (u,v)
if (visited[v] == WHITE) {
// Se v não foi visitado, aplique o algoritmo recursivamente
scc(v);
// atualize o menor nó alcançável por u se preciso
dfs_low[u] = min(dfs_low[u], dfs_low[v]);
} else if (visited[v] == GREY) {
/** Se v foi visitado, porém não finalizado, então existe uma
* back-edge de u para v, correspondendo a um ciclo, logo
* atualiza-se dfs_low com a numeração de DFS de v, caso
* necessário
**/
dfs_low[u] = min(dfs_low[u], dfs_num[v]);
}
}
/**
* Caso dfs_low[u] == dfs_num[u] então todos os nós pertencentes à
* componente fortemente conexa de u estão na pilha.
**/
if (dfs_low[u] == dfs_num[u]) {
int v;
/** Imprime os nós que compartilham a mesma componente
* fortemente conexa de u.
*/
do {
v = st.top();
st.pop();
visited[v] = BLACK;
cout << v << " ";
} while (u != v);
cout << endl;
}
}
/**
* @brief Aplica o algoritmo scc para cada nó não visitado
*/
void find_scc(){
for(size_t i=0;i<g.size();i++){
if(visited[i]==WHITE){
scc(i);
}
}
}Busca de Pontos de Articulação
No conexto de grafos não-direcionados, um ponto de articulação é um vértice $u$ cuja sua remoção ocasiona um aumento no número de componentes conexas do grafo. Por remoção de um vértice, entende-se que tanto o vértice quanto as arestas incidentes nele são removidas.
É possível utilizar um algoritmo similar ao algoritmo de detecção de componentes fortementes conexas de Tarjan para detectar pontos de articulação em um grafo. As mesmas estruturas $\mathtt{dfs\_low}$ e $\mathtt{dfs\_num}$ são utilizadas. Suponha um nó $u$ e suponha $v$ um vizinho de $u$. Se $\mathtt{dfs\_low[v]} \leq \mathtt{dfs\_num[u]}$, quer dizer que $u$ é um ponto de articulação, pois como $v$ não consegue alcançar nem um nó anterior a $u$ na árvore de DFS, ao retirar $u$, é impossível chegar a $v$. A única exceção é quando $u$ é a raiz da árvore de DFS. Neste contexto, $u$ é um ponto de articulação se e somente se possui $2$ ou mais vizinhos.
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
enum{NIL = -1, WHITE=0,GREY=1,BLACK=2};
// Variáveis globais
int dfs_n = 0; // Numeração da DFS
vector<vi> g; // Lista de adjacências
vi dfs_num; // Estrutura dfs_num
vi dfs_low; // Estrutura dfs_low
vi visited; // Marca o estado do vértice
vector<bool> articulation_vertex; // Marca quais vértices são pontos de articulação
vi parent; // Marca quem são os pais de cada nó na árvore de DFS. Inicializado com NIL.
/**
* @brief A partir de um nó u, computa os vértices de articulação
* que são alcançáveis a partir de u.
*
* @param u Nó inicial.
*/
void dfs_ap(int u) {
dfs_num[u] = dfs_low[u] = dfs_n;
dfs_n++;
// Marca u como visitado
visited[u] = BLACK;
// Número de vizinhos imediatos de u não visitados
int children = 0;
for (auto v : g[u]) {
// Para cada aresta (u,v)
if (visited[v] == WHITE) {
// Se v não foi visitado, aplique o algoritmo recursivamente
children++;
parent[v] = u;
dfs_ap(v);
// atualize o menor nó alcançável por u se preciso
dfs_low[u] = min(dfs_low[u], dfs_low[v]);
/** Se u é a raiz da DFS e possui mais de um filho,
* então u é um ponto de articulação
*/
if(parent[u] == NIL && children>1){
articulation_vertex[u] = true;
}
/** Se u não é a raiz da DFS e o vértice com numeração mais
* baixa alcançável por v é maior ou igual a numeração de u,
* então u é um ponto de articulação.
*/
if(parent[u] !=NIL && dfs_low[v]>=dfs_num[u]){
articulation_vertex[u] = true;
}
}
/** Se v já foi visitado, então (u,v) é uma back-edge. Se
* essa aresta não forma um ciclo imediato, então atualiza-se
* low[u]
*/
else if (v!=parent[u]) {
dfs_low[u] = min(dfs_low[u], dfs_num[v]);
}
}
}
/**
* @brief Aplica o algoritmo dfs_ap para cada nó não visitado
*/
void find_ap(){
for(size_t i=0;i<g.size();i++){
if(visited[i]==WHITE){
dfs_ap(i);
}
}
for(size_t i=0;i<g.size();i++){
if(articulation_vertex[i]){
cout << i << " is an articulation vertex\n";
}
}
}Detecção de Pontes
Uma ponte, no contexto de grafos não-direcionados, é uma aresta cuja sua retirada aumenta o número de componentes conexas do grafo.
Para detectar pontes, é necessário fazer uma minúscula alteração no código anterior. Supondo que $v$ é vizinho de $u$ e $\mathtt{dfs\_low[v]} >\mathtt{dfs\_num[u]}$, é correto dizer que $v$ não consegue alcançar $u$ através de outro caminho, então, se a aresta $(u,v)$ for removida do grafo, $v$ passa a não conseguir alcançar $u$ e temos um aumento no número de componentes conexas.
Atualizando o algoritmo anterior para o discutido agora, temos:
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vi = vector<int>;
using vii = vector<ii>;
enum{NIL = -1, WHITE=0,GREY=1,BLACK=2};
// Variáveis globais
int dfs_n = 0; // Numeração da DFS
vector<vi> g; // Lista de adjacências
vi dfs_num; // Estrutura dfs_num
vi dfs_low; // Estrutura dfs_low
vi visited; // Marca o estado do vértice
vi parent; // Marca quem são os pais de cada nó na árvore de DFS. Inicializado com NIL.
/**
* @brief A partir de um nó u, imprime as pontes que são alcancáveis
* alcançáveis a partir de u.
*
* @param u Nó inicial.
*/
void dfs_bd(int u) {
dfs_num[u] = dfs_low[u] = dfs_n;
dfs_n++;
// Marca u como visitado
visited[u] = BLACK;
// Número de vizinhos imediatos de u não visitados
int children = 0;
for (auto v : g[u]) {
// Para cada aresta (u,v)
if (visited[v] == WHITE) {
// Se v não foi visitado, aplique o algoritmo recursivamente
children++;
parent[v] = u;
dfs_bd(v);
// atualize o menor nó alcançável por u se preciso
dfs_low[u] = min(dfs_low[u], dfs_low[v]);
// Verifica se (u,v) é uma ponte
if(parent[u] !=NIL && dfs_low[v]>dfs_num[u]){
cout << "(" << u << "," << v << ") is a bridge\n";
}
}
/** Se v já foi visitado, então (u,v) é uma back-edge. Se
* essa aresta não forma um ciclo imediato, então atualiza-se
* low[u]
*/
else if (v!=parent[u]) {
dfs_low[u] = min(dfs_low[u], dfs_num[v]);
}
}
}
/**
* @brief Aplica o algoritmo dfs_ap para cada nó não visitado
*/
void find_bridges(){
for(size_t i=0;i<g.size();i++){
if(visited[i]==WHITE){
dfs_bd(i);
}
}
}Árvore Espalhada Mínima
Algoritmo de Kruskal
#include <bits/stdc++.h>
using namespace std;
class union_find{
public:
/**
* @brief Construtor, inicializa as estruturas
* rank e parent, além de colocar o parent[i] para
* cada elemento i
*
* @param n número de elementos
*/
union_find(int n){
rank.assign(n,0);
parent.assign(n,0);
for(int i=0;i<n;i++){
parent[i] = i;
}
}
/**
* @brief Retorna o elemento representativo do conjunto em que i
* se encontra. Utiliza os ponteiros dos pais para localizar o
* elemento representativo enquanto adota a técnica de path-compression;
*
* @param i elemento inicial
* @return int elemento representativo do conjunto em que i se encontra
*/
int find(int i){
return (parent[i]==i) ? i : (parent[i] = find(parent[i]));
}
/**
* @brief Une os conjuntos em que i e j se encontram ao fazer
* o merge entre duas árvores.
*
* @param i primeiro elemento
* @param j segundo elemento
*/
void union_set(int i,int j){
// Procura os elementos representativos de i e j
auto x = find(i);
auto y = find(j);
// Se i e j não fazem parte do mesmo conjunto, a união é feita
if(x!=y){
if(rank[x] > rank[y]){
parent[y] = x;
}
else{
parent[x] = y;
if(rank[x]==rank[y]){
rank[y]++;
}
}
}
}
/**
* @brief Verifica se i e j estão no mesmo conjunto
*
* @param i primeiro elemento
* @param j segundo elemento
* @return true caso i e j estejam no mesmo conjunto
* @return false caso contrário
*/
bool is_same_set(int i,int j){
return find(i) == find(j);
}
private:
vector<int> parent,rank;
};#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
/**
* @brief Aplica o método de kruskal sobre o grafo.
*
* @param edges um vetor contendo um par (peso, aresta), indicando
* o peso de cada aresta do grafo. Cada aresta por sua vez é identificada
* usando um par de vértices
* @param n número de vértices do grafo
* @return int o peso da árvore espalhada mínima
*/
int kruskal(vector<pair<int,ii>>& edges, int n){
int cost = 0;
// Ordena pelo peso
sort(edges.begin(),edges.end());
// Cria uma estrutura de conjuntos disjuntos de tamanho n;
union_find uf(n);
// Para cada aresta em ordem crescente de peso
for(size_t i=0;i<edges.size();i++){
/***
* Caso os vértices das arestas estejam em componentes
* distintas, a aresta tem que estar na árvore espalhada
* mínima
*/
if(!uf.is_same_set(edges[i].second.first,edges[i].second.second)){
// Adiciona o peso da aresta no custo da MST
cost += edges[i].first;
// Une os dois vértices em uma mesma componente conexa
uf.union_set(edges[i].second.first,edges[i].second.second);
}
}
return cost;
}Algoritmo de Prim
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vii = vector<ii>;
// Grafo
vector<vii> g;
// Vetor que marca os nós que já foram processados
vector<bool> processed;
/**
* @brief Processa um nó u
*
* @param pq fila de prioridades
* @param u nó a ser processado
*/
void process(priority_queue<ii>& pq,int u){
// marca u como processado
processed[u] = true;
// para cada vizinho de u
for(auto& v: g[u]){
// se o vizinho v.first não foi processado
if(!processed[v.first]){
/***
* Insira na fila de prioridades a negação do custo
* da aresta e a negação do identificador do nó vizinho.
* Utiliza-se a negação pois a priority_queue é uma heap
* de máximo.
*/
pq.push({-v.second,-v.first});
}
}
}
/**
* @brief Algoritmo de Prim
*
* @return int retorna o custo da árvore espalhada mínima
*/
int prim(){
int cost = 0;
// marca todos os nós como não processados
processed.assign(g.size(),false);
// declara uma fila de prioridades que dá o próximo nó com menor custo
priority_queue<ii> pq;
// Processa o primeiro nó
process(pq,0);
// Enquanto houver nós a serem processados
while(!pq.empty()){
// Obtém o próximo nó de menor custo
ii front = pq.top();
pq.pop();
// Restaura o peso e o id do nó ao negá-los
auto u = -front.second;
auto w = -front.first;
// Se o nó não foi processado
if(!processed[u]){
// adicione ele á MST
cost+=w;
// Processe o nó
process(pq,u);
}
}
return cost;
}Menor Caminho
Dijkstra
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vii = vector<ii>;
const int INF = numeric_limits<int>::max();
// Vetores de custo e processamento
vector<int> cost;
vector<bool> processed;
/**
* @brief Dado um grafo g e um nó de partida u, calcula o vetor
* cost, que contém o tamanho do menor caminho entre u e qualquer
* outro vértice de g
*
* @param g grafo
* @param u nó de partida
*/
void dijkstra(vector<vii>& g,int u){
// Inicializa o custo de todos os nós como infinito
cost.assign(g.size(),INF);
// Marca todos os nós como não processados
processed.assign(g.size(),false);
priority_queue<ii> pq;
// O custo do nó de partida só pode ser zero
cost[u] = 0;
// Insere o nó de partida na fila de prioridades
pq.push({-cost[u],u});
// Enquanto houver nós a serem retirados da fila de prioridades
while(!pq.empty()){
// Obtém o próximo nó de menor custo
int v = pq.top().second;
// Remove o nó da fila de prioridades
pq.pop();
// Se o nó já foi processado, pule esta iteração
if(processed[v]){
continue;
}
// Marque o nó como processado
processed[v] = true;
/***
* Para cada vizinho w de v, verifique a condição de relaxamento,
* isto é, se o custo de u até w for maior do que o custo de u
* até v mais o peso da aresta (v,w), atualize o custo de u até
* w.
***/
for(auto& w: g[v]){
if(!processed[w.first] && cost[w.first] > cost[v]+w.second){
cost[w.first] = cost[v] + w.second;
/***
* Após a atualização, insira o nó w com o custo atualizado
* na fila de prioridades. Aqui inserimos a negação do custo
* pois por padrão, a fila de prioridades é uma heap de
* máximo
***/
pq.push({-cost[w.first],w.first});
}
}
}
}Bellman-Ford
#include <bits/stdc++.h>
using namespace std;
using ii = pair<int,int>;
using vii = vector<ii>;
/***
* Dividimos por dois para evitar overflow na soma
* de um valor INF com um valor positivo.
***/
const int INF = numeric_limits<int>::max()/2;
vector<int> cost;
/**
* @brief Aplica o método de Bellman-Ford no grafo g para calcular
* o custo do menor caminho entre u e qualquer outro nó de g
*
* @param g Grafo
* @param u Nó de partida
*/
void bellman_ford(vector<vii>& g,int u){
cost.assign(g.size(),INF);
// Inicializa o custo de u para ele mesmo
cost[u] = 0;
/***
* Aplica o método de bellman ford: para cada aresta, aplique
* a condição de relaxamento. Isso deve ser repetido |V| - 1 vezes,
* pois um caminho possui no máximo |V|-1 arestas.
***/
for(size_t k=0;k<g.size()-1;k++){
for(size_t u=0;u<g.size;u++){
for(auto& v: g[u]){
cost[v.first] = min(cost[v.first],cost[u]+v.second);
}
}
}
/***
* Realiza uma última verificação para checar se existem ciclos
* negativos no grafo
***/
bool has_negative_cycle = false;
for(size_t u=0;u<g.size();u++){
for(auto& v: g[u]){
if(cost[u]+v.second < cost[v.first]){
has_negative_cycle = true;
}
}
}
}Floyd-Warshall
#include <bits/stdc++.h>
using namespace std;
using vi = vector<int>;
// Dividimos por 2 para evitar overflow na soma entre dois valores INF
const int INF = numeric_limits<int>::max()/2;
/**
* @brief Dado um grafo representado por uma uma matrix de
* adjacências, calcule o menor caminho entre quaisquer par de vértices.
* Ao término do algoritmo, a matriz de adjacências na posição g[u][v]
* contém o custo do menor caminho entre u e v;
*
* @param g Grafo representado por uma matriz de adjacências
*/
void floyd_warshall(vector<vi>& g){
/***
* Caso base, o custo de cada nó para ele mesmo é zero e o custo
* de todo nó u para todo nó v conectado por uma aresta (u,v) é o
* peso da aresta (u,v). Caso contrário, o custo de u para v é infinito.
***/
for(size_t i=0;i<g.size();i++){
for(size_t j=0;j<g.size();j++){
/***
* Se não existe aresta de i para j, então a distância de
* i para j é sinalizada como infinito
***/
if(g[i][j]==-1){
g[i][j] = INF;
}
}
// Distância de um nó para ele mesmo é 0
g[i][i] = 0;
}
/***
* Calcula a menor distância entre todos os nós utilizando
* os nós {0,1,2,...,k}
***/
for(int k=0;k<g.size();k++){
for(int i=0;i<g.size();i++){
for(int j=0;j<g.size();j++){
g[i][j] = min(g[i][j],g[i][k]+g[k][j]);
}
}
}
}